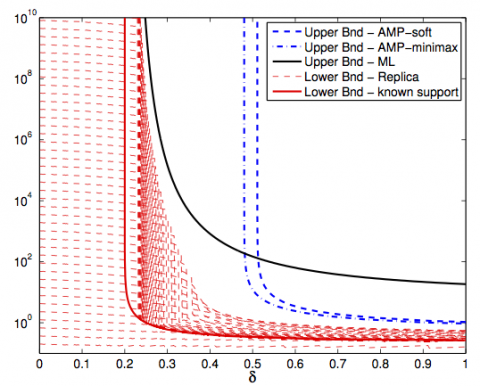
Successful high-resolution signal reconstruction — in problems ranging from astronomy to biology to medical imaging — depends crucially our ability to make the most out of indirect, incomplete, and inaccurate data. A large and active area of research, known as compressed sensing, has drawn researchers from applied mathematics, information theory, mathematical statistics, and optimization theory to focus on the design and analysis of computational reconstruction methods. These methods take advantage of low dimensional structure inherent in the data (e.g. sparsity, low rank) to overcome that fact that the number of unknowns may far exceed the number of knowns .
In this project, we build upon a key theoretical insight about signal recovery from undersampled data: In many cases, the effect on the end user is the same as if each component of the unknown signal had been observed directly after being corrupted by independent random noise. Using this insight as a guiding principle, we give precise answers to a variety of key engineering questions concerning the relaxation of model assumptions, the minimax sensitivity to noise, and the design of near-optimal adaptive strategies which learn the statistics of the underlying data.