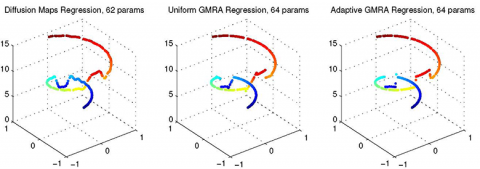
We present a framework for high-dimensional regression using the GMRA data structure. In analogy to a classical wavelet decomposition of function spaces, a GMRA is a tree-based decomposition of a data set into local linear projections.
Moreover, for new points, GMRA admits a fast algorithm for computing the projection coefficients on the already-learned dictionary. Within each node of the tree one can also assign regression coefficients in any manner; here we study the simple case of weighted linear regression. We explore the performance of the method using synthetic data as well as galactic spectra from the Sloan Digital Sky Survey, and compare against other methods for regression in high dimensions.
Contact
David Lawlor
Mathematics
djl@math.duke.edu
Mathematics
djl@math.duke.edu
